無料ダウンロード オイラー の 公式 美 しさ 106433-美 しさ オイラー の 公式

オイラーの公式は、また、三角関数の様々な基本公式を容易に導き出すのに有効 である。ここでは、 および を使う。 負角の公式 および であり、 補角の公式 および 余角の公式 および 補角の公式同様、 加法定理 および であり、 と の相補関係オイラーの公式 崎間＠物理のかぎプロジェクト さりげなく多用されているオイラーの公式は，複素数と実数の橋渡しとしてかなり重要です．オ イラーの公式はつぎの形をしています． eiax = cos(ax) isin(ax) (1)資料請求番号：TS39 博士の愛した数式「オイラーの公式」を導出する オイラーの公式を表現した国語 小川洋子さんの小説、博士の愛した数式には、このような文章があります。 果ての果てまで循環する数と、決して正体を見せない虚ろな数が簡潔な軌跡を描き、一点に着地する。どこにも円は

オイラーの公式 世界一美しい数式を証明せよ ちょっと背伸びな高校数学 1 2 Youtube

美 しさ オイラー の 公式

美 しさ オイラー の 公式-数学の複素解析におけるオイラーの公式（オイラーのこうしき、英 Euler's formula ）とは、複素指数函数と三角関数の間に成り立つ、以下の恒等式のことである： = ここで e · は指数関数、 i は虚数単位、 cos ·, sin · はそれぞれ余弦関数、正弦関数（三角関数）である。特に a = 0 a=0 a = 0 の場合をオイラーの公式と呼びます： e i θ = cos ⁡ θ i sin ⁡ θ e^{i\theta}=\cos\thetai\sin\theta e i θ = cos θ i sin θ 更に，オイラーの公式に θ = π \theta=\pi θ = π を代入すれば有名なオイラーの等式（博士の愛した数式）を得ることができます

オイラーの等式 Wikipedia

オイラーの公式 e iχ ＝cosχ＋i sinχ はじめて見た時、意味がわかりませんでした。eって何？ i 乗ってできるの？ ･･･しばらくして微分方程式を学習した時、なんてすごい公式だろうと思いました。オイラーの公式 e iχ ＝cosχ＋i sinχ はじめて見た時、意味がわかりませんでした。eって何？ i 乗ってできるの？ ･･･しばらくして微分方程式を学習した時、なんてすごい公式だろうと思いました。レオンハルト・オイラー（Leonhard Euler, 1707年 4月15日 17年 9月18日）は、18世紀の数学者・天文学者（天体物理学者）。 18世紀の数学界の中心となり、続く19世紀の厳密化・抽象化時代の礎を築いた 。 数学者としての膨大な業績と、後世の数学界に与えた影響力の大きさから、19世紀のカール

数学誌(The Mathematical Intelligencer)の読者調査で「数学における最も美しい定理(The most beautiful theorem in mathematics)」に選出されたオイラーの等式についオイラーの公式 公式 オイラーの公式実数θ に対しeiθ = cosθ isinθ とすると ei·0 = cos0isin0 は実数に対し 指数公式 微分積分・同演習A – p2/15オイラーの等式とは？ 天才数学者「レオンハルト・オイラー」が導出した等式 「数学界におけるもっとも美しい等式」と言われています もちろんぼくも「 数学の一番有名で美しい等式は何か」と聞かれたらこの等式を挙げるでしょうね この等式は理系学生であれば誰でも知っているような

1 オイラーの公式 11 オイラー レオンハルト・オイラー(1707–17)はスイスの数学者。ヨハン・ ベルヌーイに師事して数学を学んだ。人並み外れた記憶力と計算力 を持っていたオイラーは，「人が呼吸するように，鷲が空を舞うよう に計算した」と評された。オイラーの公式 expiθ=cosθisinθなのに、 なんでexpiωt=sin(ωt)と書けるんでしょうか？ 向けの数学の本に e^iπ＋1＝0 という式が紹介されており、筆者がこの式は数学の美と調和と不思議を示すものとして自分の墓誌に刻んだと書いてありましたオイラーの公式 常微分方程式にしても偏微分方程式にしても、それらの解はおおかた指数函数か 三角函数の組合わせで書かれる。そこで、まず、復習として、指数函数と三角函 数の結び付きを示すオイラーの公式から始める。

オイラーの公式の三次元化

数学の美しさ オイラーの公式から消えた年金記録相殺マジック 発想力教育研究所 素数誕生のメカニズム

オイラーの公式の使い方 高校数学では習わないオイラーの公式ですが、知っていると役に立つ場面もあります。 ここでは、オイラーの公式の活用方法をいくつか紹介します。 極形式の複素数同士の計算を楽にできるこの記事は物理数学の直観的方法の4章の自分なりの平凡なまとめを淡々と描くものです。過度な期待はしないでください。 オイラーの公式は以下の式ですね。 e^{i\\theta}=\\cos\\thetai\\sin\\theta 右辺オイラーの公式は人類が発見した方程式でも最も美しい方程式と言っても過言ではない。 次にオイラーの公式の証明を行う。 オイラーの公式の証明 数学者であり、天文学者であるレオンハルト・オイラーは\( e^{i \theta} \)と三角関数の級数展開（一定の規則

世界一美しい数式 Eip 1 を証明する Jmam 日本能率協会マネジメントセンター 人 組織 経営の変化 を支援するjmamの書籍

数学者がオイラーの等式の美しさを称える理由 ワイズ

Amazonで原岡 喜重のオイラーの公式がわかる (ブルーバックス)。アマゾンならポイント還元本が多数。原岡 喜重作品ほか、お急ぎ便対象商品は当日お届けも可能。またオイラーの公式がわかる (ブルーバックス)もアマゾン配送商品なら通常配送無料。「オイラーの座屈理論公式」とは？ web2CAD 用語集 材料力学 の「オイラーの座屈理論公式」に関する説明ページです。1階常微分方程式 y'=F(x,y)の解 y=f(x)をオイラー法で求めます。初期条件 y0=f(x0)でxを x0≦x≦xnの範囲で求めます。

世界一美しい数式でどこが美しいのか解りませんできたら教えてください Yahoo 知恵袋

オイラーの公式がわかる 感想 レビュー 試し読み 読書メーター

ベキ関数の和によっていろいろな関数を作ることができます。 これを自在に作るためにはどうしたら良いのでしょうか？ 今度は、ある関数は無限のベキ関数の級数に表すことができるとしましょう。 そうすると、微分をすることで、それぞれの係数を求めることができます。ブリタニカ国際大百科事典 小項目事典 オイラーの定理の用語解説 (1) オイラーの多面体定理ともいう。単純な多面体すなわち「凸多面体において，その頂点の数を v ，辺の数を e ，面の数を f とすれば，これらの数の間には v－e＋f＝2 という関係が成り立つ」。1 オイラーの公式 11 オイラー レオンハルト・オイラー(1707–17)はスイスの数学者。ヨハン・ ベルヌーイに師事して数学を学んだ。人並み外れた記憶力と計算力 を持っていたオイラーは，「人が呼吸するように，鷲が空を舞うよう に計算した」と評された。

美しさ おとなぱすた

オイラーの公式 の美しさを数学以外の分野で例えるならどれほど美しさに匹敵すると思いますか Quora

特に a = 0 a=0 a = 0 の場合をオイラーの公式と呼びます： e i θ = cos ⁡ θ i sin ⁡ θ e^{i\theta}=\cos\thetai\sin\theta e i θ = cos θ i sin θ 更に，オイラーの公式に θ = π \theta=\pi θ = π を代入すれば有名なオイラーの等式（博士の愛した数式）を得ることができますオイラーの公式 e iχ ＝cosχ＋i sinχ はじめて見た時、意味がわかりませんでした。eって何？ i 乗ってできるの？ ･･･しばらくして微分方程式を学習した時、なんてすごい公式だろうと思いました。ブリタニカ国際大百科事典 小項目事典 オイラーの定理の用語解説 (1) オイラーの多面体定理ともいう。単純な多面体すなわち「凸多面体において，その頂点の数を v ，辺の数を e ，面の数を f とすれば，これらの数の間には v－e＋f＝2 という関係が成り立つ」。

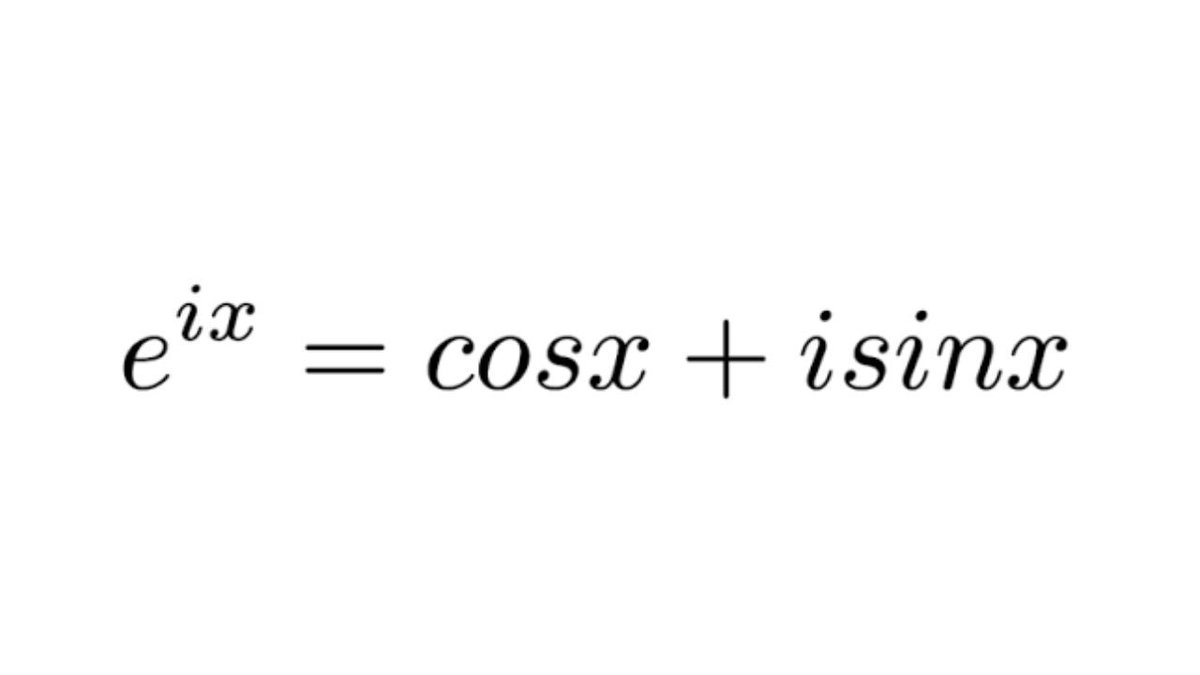
山口慶明 で何とか生きてる 疲れたのでオイラーの公式を見て癒されよう ああ さすが人類至上最も美しいと言われる公式 美しい 実数の世界では赤の他人と思われていた三角関数と指数関数が 虚数の世界を通じて繋がっていた もうロマンチックが過ぎる

数学 のアイデア 12 件 数学 オイラー 数式

オイラーの公式は、また、三角関数の様々な基本公式を容易に導き出すのに有効 である。ここでは、 および を使う。 負角の公式 および であり、 補角の公式 および 余角の公式 および 補角の公式同様、 加法定理 および であり、 と の相補関係オイラーの公式とは まず オイラーの公式 とは つぎのような公式をさします。 $$\Large e^{i\theta}=\cos \theta i \sin \theta$$ これは数Ⅲで学習する内容で 複素数平面で大活躍してくれます。 なぜこの公式が成り立つか というのは勉強する必要はありませんが

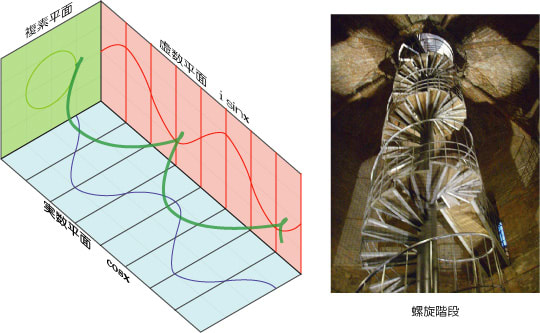
博士の愛した数式は本当に美しい オイラー公式の美しさを現実的に図解すると 皮膚呼吸しか知らない蛙

三角関数と指数関数が 虚数 複素数を通じて表裏一体の関係 オイラーの公式 ド モアブルの定理

オイラーの公式

オイラーの公式 の美しさを数学以外の分野で例えるならどれほど美しさに匹敵すると思いますか Quora

科学と芸術 掲示第2弾 京都学園高等学校

オイラーの公式 クライネだより

オイラーの等式はなぜ美しいのか Youtube

第22話 天下無双の不変の関数は宇宙を支配する オイラー数e コサインなんて人生に必要ないと思った人のための数学のはなし

数学 小学生でもわかる オイラーの等式 セントラル ステーション分室

美しい数式図鑑 No 1 オイラーの等式 ナウシカ Note

ファイは月に吼える

数研出版 マグカップ オイラーの公式 Ver 2 雑貨通販 ヴィレッジヴァンガード公式通販サイト

Amazon クリアファイル オイラーの公式 数研グッズ クリアホルダー 文房具 オフィス用品

三角関数と指数関数が 虚数 複素数を通じて表裏一体の関係 オイラーの公式 ド モアブルの定理

数学の美しさ オイラーの公式から消えた年金記録相殺マジック 発想力教育研究所 素数誕生のメカニズム

複素数入門 フィズヨビ

オイラーの公式とは 証明やオイラーの等式との関係 受験辞典

Www Iwanami Co Jp Files Tachiyomi Pdfs Pdf

美しい数式図鑑 No 1 オイラーの等式 ナウシカ Note

オイラーの公式 世界一美しい数式を証明せよ ちょっと背伸びな高校数学 1 2 Youtube

中学の知識でオイラーの公式がわかる

オイラーの公式とは 証明やオイラーの等式との関係 受験辞典

楽天ブックス オイラーの贈物 吉田武 数理工学 本

数研出版 マグカップ オイラーの公式 雑貨通販 ヴィレッジヴァンガード公式通販サイト

複素数はなぜ 究極の数 なのか 虚数からオイラーの公式まで 示野 信一 ブルーバックス 講談社

三角関数と指数関数が 虚数 複素数を通じて表裏一体の関係 オイラーの公式 ド モアブルの定理

美しい数式図鑑 No 1 オイラーの等式 ナウシカ Note

オイラーの公式とは何か オイラーの等式の求め方の流れを紹介 我々の至宝と評された公式 アタリマエ

超わかる オイラーの公式を見て 聞いて 感じるンゴ Love ９タイプス

オイラーの等式はなぜ美しいのか Youtube

オイラーの等式 Wikipedia

オイラーの等式 Euler S Identity Japaneseclass Jp

数学者がオイラーの等式の美しさを称える理由 ワイズ

重要な数を詰め込みまくったオイラーの等式 式模様

数学者がオイラーの等式の美しさを称える理由 ワイズ

Amazon クリアファイル オイラーの公式 数研グッズ クリアホルダー 文房具 オフィス用品

数学者がオイラーの等式の美しさを称える理由 ワイズ

その1 驚き 正n角形の1頂点から他の頂点までの全線分の積はn

中学の知識でオイラーの公式がわかる 鈴木貫太郎 光文社新書 ソニーの電子書籍ストア Reader Store

オイラーの公式 Instagram Posts Photos And Videos Picuki Com

オイラーの公式を崇めるだけ タイピング練習の マイタイピング

オイラーの等式よりも美しい Qiita

オイラーの公式とトポロジー Sgk Note

小川洋子 博士の愛した数式 私撰アンソロジー ３１ 夢幻と湧源

オイラーの公式とは 証明やオイラーの等式との関係 受験辞典

数学者がオイラーの等式の美しさを称える理由 ワイズ

数学の言葉で世界を見たら 付録 Hirosi Ooguri

中学の知識でオイラーの公式がわかる 光文社新書 鈴木貫太郎 の感想 7レビュー ブクログ

美しいオイラーの等式をやっと理解 わけいブログ

超わかる オイラーの公式を見て 聞いて 感じるンゴ Love ９タイプス

科学と芸術 掲示第2弾 京都学園高等学校

超わかる オイラーの公式を見て 聞いて 感じるンゴ Love ９タイプス

オイラーの公式とは何か オイラーの等式の求め方の流れを紹介 我々の至宝と評された公式 アタリマエ

Amazon Tシャツ オイラーの公式 オリジナルプリント 通販

Q Tbn And9gcr0bhg5c7ghgomygyp7kvpwftgj65uwlmjvqwa549bbnffz R Usqp Cau

織田曜一郎 Oda Yoichiro Auf Twitter 数式でも 世界一美しい公式 ってのがあるらしいが これなんかはさっぱり私には美しさが分からない 短い式だな と思うが 私の数学は虚数が理解できないところで止まってるので 何が何だかわからない

楽天ブックス 中学の知識でオイラーの公式がわかる 鈴木貫太郎 本

なっとくする数学記号 P ｅ ｉから偏微分まで 漫画 無料試し読みなら 電子書籍ストア ブックライブ

オイラーの公式とは何か オイラーの等式の求め方の流れを紹介 我々の至宝と評された公式 アタリマエ

数研出版 サコッシュ オイラーの公式 雑貨通販 ヴィレッジヴァンガード公式通販サイト

Q Tbn And9gcsffgj6427vcxojcu W13r6taeevcuxgekpqfcz54u8 Xkwor2o Usqp Cau

オイラーの公式

Q Tbn And9gcqvvpzmbx0yf5pyydlbophfdt9gyojals Kuf12hodw9nkvw1 Usqp Cau

数学の美しさ オイラーの公式から消えた年金記録相殺マジック 発想力教育研究所 素数誕生のメカニズム

数学の美しさ メモ Of 高校数学 A なっとくの微積 解析 仮題

オイラーの公式とは何か オイラーの等式の求め方の流れを紹介 我々の至宝と評された公式 アタリマエ

数学で最も美しい定理 オイラーの等式

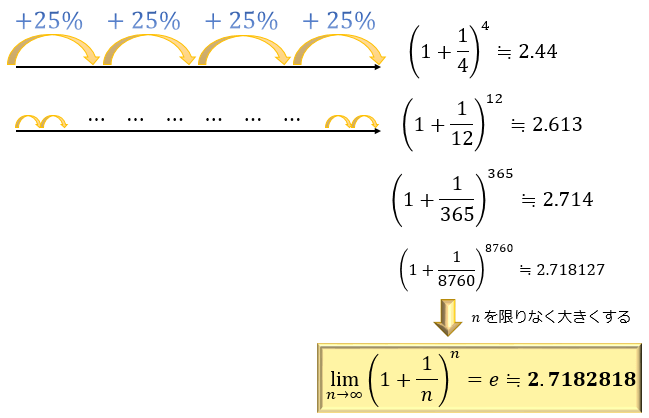
オイラーの公式とは何か オイラーの等式の求め方の流れを紹介 我々の至宝と評された公式 アタリマエ

オイラー Instagram Posts Photos And Videos Picuki Com

数学の美しさが目に見えるアート エキサイトニュース

オイラーの公式と数学の美しさについて そして少しだけ英語 数学が好きなサラリーマンのブログ

新装版 オイラーの贈物ー人類の至宝e Ip 1を学ぶ 感想 レビュー 読書メーター

博士の愛した数式 オイラーの公式 最強 受験 学習相談所 In 楽天 楽天ブログ

オイラーの等式 Wikiwand

なぜ オイラーの等式 は最も美しい数式と言われているのでしょうか Quora

数研出版 クリアファイル オイラーの公式 雑貨通販 ヴィレッジヴァンガード公式通販サイト

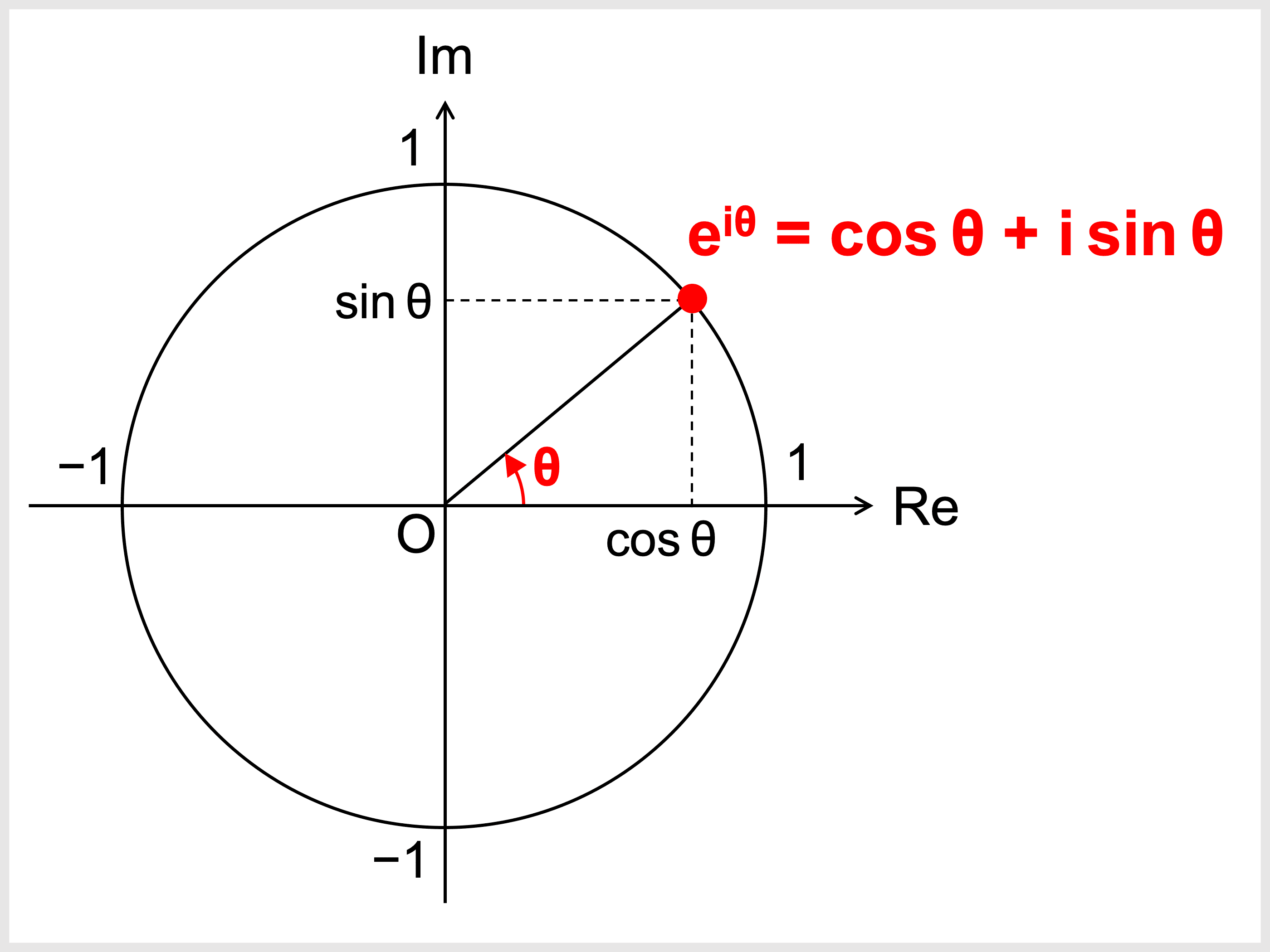
Tvhhgqmiko8dvm

Amazon Tシャツ オイラーの公式 オリジナルプリント 通販

オイラーの公式 数学美術館

超わかる オイラーの公式を見て 聞いて 感じるンゴ Love ９タイプス

数学の美しさ オイラーの公式から消えた年金記録相殺マジック 発想力教育研究所 素数誕生のメカニズム

数学の美しさについて

博士の愛した数式とオイラーの等式とオイラーの公式が組合わせ爆発 スパイス カフェマスターのブログ

東大生が語る ちょっとディープな美しすぎる数式の話 東京大学cast ブルーバックス 講談社 1 3

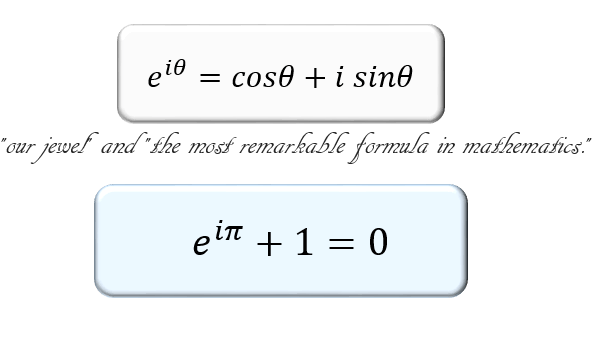
オイラーの公式とは何か オイラーの等式の求め方の流れを紹介 我々の至宝と評された公式 アタリマエ

中学の知識でオイラーの公式がわかる 本がすき 本がすき

数研出版 シャープペン オイラーの公式 雑貨通販 ヴィレッジヴァンガード公式通販サイト

感銘を受けた数学 オイラーの五角数定理 数学 統計教室の和から株式会社

オイラーの等式 Wikipedia

中学の知識でオイラーの公式がわかるの通販 鈴木 貫太郎 光文社新書 紙の本 Honto本の通販ストア

Q Tbn And9gcqdwensn Gkhcpyst1nqtgrlzubrjvjnndxqulm3t4 Usqp Cau

オイラー

第22話 天下無双の不変の関数は宇宙を支配する オイラー数e コサインなんて人生に必要ないと思った人のための数学のはなし

新装版 オイラーの贈物ー人類の至宝e Ip 1を学ぶ 吉田 武 本 通販 Amazon

Incoming Term: 美 しさ オイラー の 公式,